企业生存风险如何预测？

——

最近誉存科技的数据科学家们在模型开发中又取得了一项新的进展。通过引进Cox回归分析，进一步优化了企业失信、破产预测模型，使得我们对企业风险变化的预测，可以随时间的变化而相应变化，最终获得更为科学动态的预测结果。

一、为什么选择Cox回归分析？

Cox回归模型，又称比例风险回归模型(Proportional hazards model）。1972年，由英国统计学家D.R.Cox提出，是一种半参数回归模型。

该模型以生存结局和生存时间为应变量，可同时分析众多因素对生存期的影响。它不仅考虑事件是否发生，也考虑事件发生出现的时间，能分析带有截尾生存时间的数据，且不要求估计数据的生存分布类型。自问世以来，Cox回归在医学随访研究中受到广泛应用，是迄今生存分析中应用最多的多因素分析方法。
 

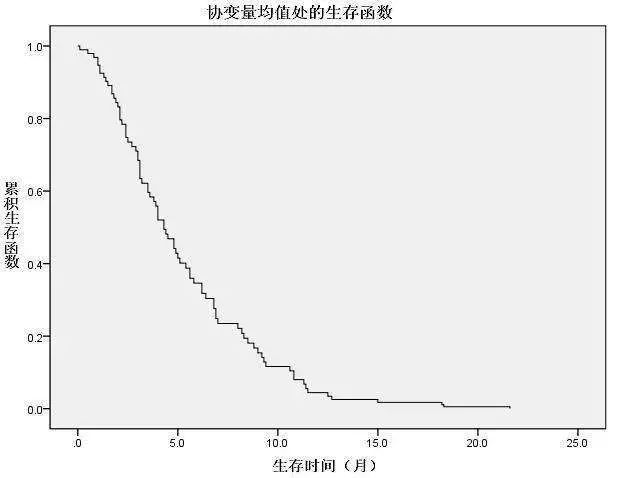
综上所述，我们可以很清晰的明了，医学随访研究与企业风险预测其实在本质上是相通的，都是关于主体生存资料的分析。

同时，我们也发现，那些基于常规分析模型所做的企业风险预测，往往会存在两个问题：

1、历史数据的标签一般基于当前状态来判断，没有考虑时间的变量；

2、模型输出值仅为当前发生风险的概率，不涉及未来一段时间内的风险概率。

所以，如果引入Cox回归分析构建关于企业生存的分析模型，我们就能加入更多基于时间的变量因素，预测出未来一段时间内企业发生失信、破产等风险的概率。
 

二、Cox回归模型的理论推导

Cox回归模型的基本原理

生存分析是将结局或终点事件和出现这一结局所经历的时间结合起来分析的一种统计方法。
 

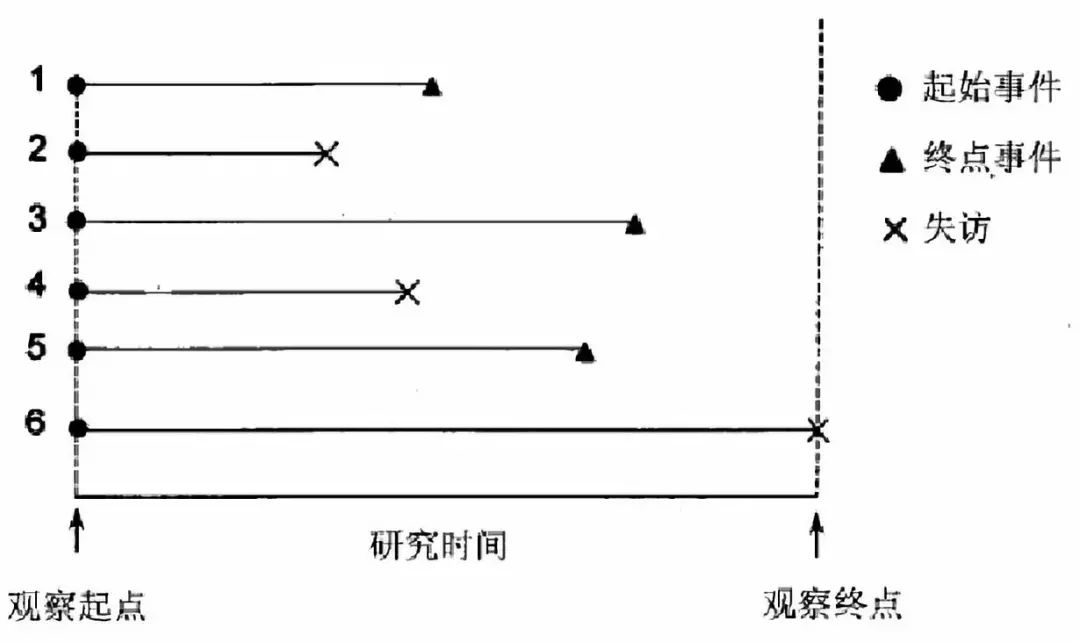
首先，我们需要明确生存分析中常用的6个术语，如下：

（1）起始事件：反应研究对象开始生存过程的起始特征事件。         

（2）终点事件：出现研究者所关心的特定结局。

（3）观察时间：从研究开始观察到研究观察结束的时间。

（4）生存时间：观察到的存活时间。

（5）完全数据：从观察起点到死亡事件所经历的时间，生存时间是完整的。

（6）截尾数据：观察时间不是由于终点事件而结束的，而是由于失访、死于非研究因素、观察结束以上三种原因结束而对象仍存活的。
 

Cox回归分析的一般条件

①比例风险假定：即PH假定，常通过观察自变量分组的Kaplan-Meier生存曲线。若曲线无明显的交叉，则提示满足PH假定。

②样本含量：一般需要协变量的15~20倍的阳性结局事件数。
 

Cox回归的风险函数公式

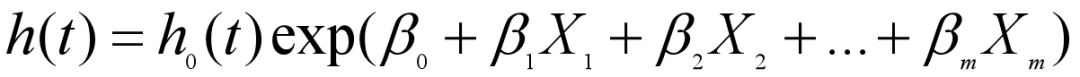
其中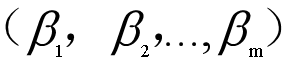，是线性模型的系数(未知参数)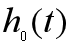，是基准风险函数，exp(...)这个式子描述了企业主体观察到回归变量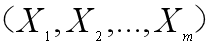的破产风险比例；式中h(t)是具有协变量x的个体在时刻t的风险函数，t表示生存时间。∀i∈N,βi>0，表示该协变量是危险因素，越大使得生存时间越短。∀i∈N,βi  

三、Cox回归模型的应用案例

我们的模型研究以企业发生失信或破产为结局，各类风险参数为主要研究因素，欲了解哪个参数对企业主体的生存影响更大，即可应用Cox比例风险模型进行分析。

下面，以企业破产风险预测为例：

>>> 预测某公司在未来时间段的破产概率

1. 样本

正样本：2W个 （随机抽取的未破产公司）

负样本：3707个 （从破产公告中解析出来）

2. 提取特征

包含司法类、股东类、法人类、工商类等数十个特征

3. 训练模型

模型的数据预处理流程跟一般的模型分析类似，如下图所示：

本次模型构建最优训练步长为0.05, 得到模型的综合评价指标Concordance =0.756，表明具有较好的区分度。同时，从模型的输出结果可以看出最终有14个特征具有统计学上显著意义。比如，一个企业作为被告身份涉及的诉讼次数（defendant_judgedoc_cnt），法人的关联企业涉及的执行次数（network_fr_zhixing_cnt）对企业风险影响较大。

进一步地，利用Cox模型我们还可以考察单一因素对企业风险的影响，例如：

（1）“成立年限”对破产预测模型的影响：成立年限越长，其相对的风险越大。

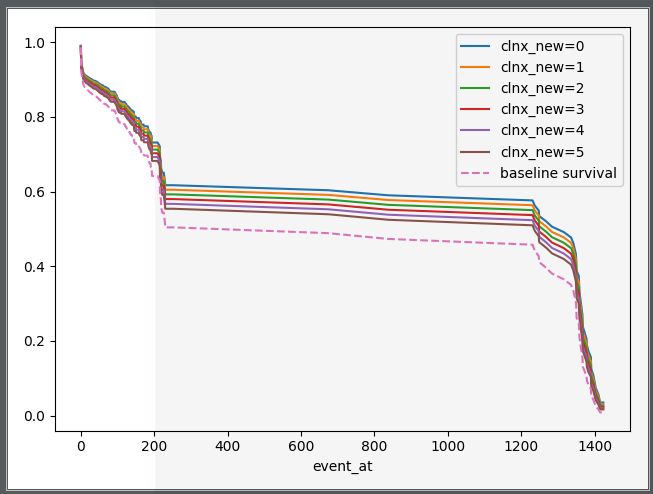
（2）“股东变更次数”对企业破产风险的影响：股东变更次数越多对企业风险影响也越大。

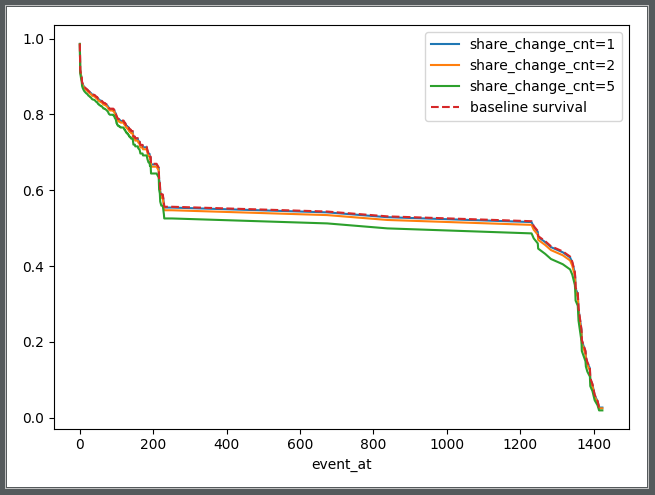
此外，需了解一点。在实际应用中，Cox回归的结局不一定就是破产或者失信，还可能表现为跑路、行政处罚、工商吊销等，不同的时间周期会表现出不一样的结果。

四、备注

在进行Cox回归分析前，如果样本不多而变量较多，建议先通过单变量分析考察所有自变量与因变量之间的关系，筛掉一些可能无意义的变量，再进行多因素分析，以保证结果更加可靠。另外，即使样本足够大，也不建议把所有的变量放入方程直接分析，一定要先弄清楚各个变量之间的相互关系，确定自变量进入方程的形式，这样才能进行有效的分析。